LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

Nama : Meidianti Sherli Rahmi

Kelas : X-MIPA 3

Absen :17

Matematika Wajib, SMAN 63 Jakarta 

LUAS SEGITIGA DENGAN TRIGONOMETRI, ATURAN SINUS DAN ATURAN COSINUS

Aturan Sinus  dan  Aturan Cosinus  merupakan dua aturan yang menghubungkan panjang sisi dan besar sudut dalam segitiga sembarang dengan menggunakan konsep trigonometri. Sesuai dengan namanya, Aturan Sinus melibatkan fungsi sinus, sama halnya dengan Aturan Cosinus. Selain itu,  luas segitiga ternyata dapat ditentukan dengan menggunakan bantuan trigonometri , yaitu berdasarkan besar sudut dan panjang dua sisi yang mengapitnya.

Aturan Sinus 

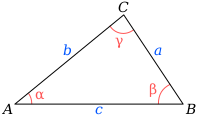
hubungan antara perbandingan panjang sisi yang berhadapan dengan sudut terhadap sudut sinus pada segitiga.  Berdasarkan aturan sinus dalam segitiga ABC, perbandingan panjang sisi dengan sinus sudut yang berhadapan dengan sisi segitiga memiliki nilai yang sama. Seperti yang dijelaskan pada gambar di bawah ini.


sinus dan kosinus

Segitiga sembarang ABC

Keterangan :

a = panjang sisi a

A = besar sudut di hadapan sisi a

b = panjang sisi b

B = besar sudut di hadapan sisi b

c = panjang sisi c

C = besar sudut di hadapan sisi c

sinus.png










Aturan Sinus

Aturan Sinus (Law of Sines atau Sines Law/Rule) adalah teorema berupa persamaan yang menghubungkan nilai sinus sudut dalam segitiga dengan panjang sisi di depannya dalam bentuk perbandingan.
Jika diberikan segitiga sembarang ABC ABC seperti gambar, maka berlaku persamaan berikut.


dengan RR adalah panjang jari-jari lingkaran luar segitiga ABC

Aturan Cosinus 

Aturan Cosinus merupakan aturan yang menjelaskan hubungan antara kuadrat panjang sisi dengan nilai cosinus dari salah satu sudut pada segitiga. Aturan cosinus dapat digunakan untuk menentukan unsur-unsur lain dalam suatu segitiga sembarang untuk dua kasus yaitu saat tiga sisi ketahui dan saat dua sisi dan sudut apitnya diketahui. Seperti yang dijelaskan pada gambar di bawah ini.


cosinus.png

Segitiga sembarang Δ ABC

Keterangan:

a = panjang sisi a

A = besar sudut di hadapan sisi a

b = panjang sisi b

B = besar sudut di hadapan sisi b

c = panjang sisi c

C = besar sudut di hadapan sisi c 

cosinuss.png















Sehingga aturan cosinus berlaku untuk setiap segitiga ABC sebagai berikut :

a2 = b2 + c2 - 2 bc cos A

b2 = c2 + a2 - 2 ac cos B

c2 = a2 + b2 - 2 ab cos C

Berdasarkan rumus aturan cosinus di atas, maka di dapatkan rumus untuk menghitung besar sudutnya :

coss.png

Aturan Cosinus

Aturan Cosinus (Law of Cosines atau Cosines Formula/Rule) adalah teorema yang digunakan untuk menentukan panjang sisi depan suatu sudut dengan menggunakan hubungan dua panjang sisi pengapit sudut tersebut dan nilai cosinusnya.


Pada segitiga ABCABC di atas, berlaku : 

Aturan Luas Segitiga dalam Trigonometri

Misalkan △ABC ΔABC segitiga sembarang seperti gambar.


Dengan demikian, luas △ABCΔABC dapat dihitung dengan rumus berikut apabila diketahui panjang dua sisi segitiga beserta besar sudut pengapitnya.


Luas segitiga juga dapat dihitung bila diketahui panjang satu sisi dan besar tiga sudutnya.

CONTOH SOAL ATURAN SINUS DAN COSINUS 

A. ATURAN SINUS

  • Sebuah segitiga diketahui memiliki sudut A = 30º, sisi a = 3 dan sisi b = 4. Hitung besar sudut B, besar sudut C dan panjang sisi c!

Diketahui:

A = 30º

a = 3

b = 4

Ditanya: B, C dan c?

Jawab:

  • Menentukan besar sudut B

soal sinus.png

Karena sinus harus bernilai positif baik di kuadran I maupun kuadran II, maka sudut lain yang memenuhi adalah B = (180º - 41,8º) = 138,2º

  • Menentukan besar sudut C

Jumlah sudut-sudut dalam segitiga adalah 180º, oleh karena itu berlaku:

A + B + C = 180º → C = 180º - (A + B)

Untuk B = 41,8º → C = 180º - (30º + 41,8º) = 108,2º

Untuk B = 138,2º → C = 180º - (30º + 138,2º) = 11,8º

  • Menentukan panjang sisi C

sinusss.png

B. ATURAN COSINUS

  • Segitiga ABC diketahui panjang sisi a = 5 cm, panjang sisi c = 6 cm dan besar sudut B = 60º. Tentukan panjang sisi b!

Diketahui:

a = 5 cm

c = 6 cm

B = 60º

Ditanya: b?

Jawab:

 b2 = a2 + c2 - 2ac cos B

 b2 = 52 + 62 - 2(5)(6) cos 60º

 b2 = 25 + 36 - 60 (0,5)

 b2 = 61 - 30

 b2 = 31

 b = 5,56 cm

Jadi, panjang sisi b adalah 5,56 cm

DAFTAR PUSTAKA :


Comments

Post a Comment

Popular posts from this blog

FUNGSI: KUADRAT, RASIONAL, IRASIONAL

Image
  Nama : Meidianti Sherli Rahmi Kelas  : X-MIPA 3 Absen :17 Matematika Wajib, SMAN 63 Jakarta FUNGSI: KUADRAT, RASIONAL, IRASIONAL Fungsi Kuadrat Fungsi kuadrat  adalah suatu persamaan dari variabel yang mempunyai pangkat tertinggi dua. Fungsi ini berkaitan dengan persamaan kuadrat. Bentuk umum persamaan kuadrat adalah:   Sedangkan bentuk umum dari fungsi kuadrat adalah: Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta  . Fungsi kuadrat f(x) dapat juga ditulis dalam bentuk y atau: Grafik Fungsi Kuadrat Fungsi kuadrat   dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola. Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y. Kemudian pasangan nilai (x, y) tersebut menjadi koordinat dari yang dilewati suatu grafik. Sebagai contoh, grafik dari
Read more

SISTEM PERSAMAAN KUADRAT-KUADRAT DAN BEBERAPA CONTOH SOALNYA

Image
Nama : Meidianti Sherli Rahmi Kelas  : X-MIPA 3 Absen : 17 Matematika Wajib, SMAN 63 Jakarta Definisi dan Bentuk Umum Sistem Persamaan Kuadrat-Kuadrat (SPKK) Sistem Persamaan Kuadrat Kuadrat atau disingkat dengan SPKK merupakan sistem persamaan yang terdiri atas dua persamaan kuadrat yang masing-masing memuat dua variabel. SPKK memiliki beberapa macam bentuk, tetapi saya akan membahas bentuk yang paling sederhana, yaitu kedua persamaan kuadrat berbentuk eksplisit. Bentuk umumnya adalah sebagai berikut. y = ax² + bx + c …… (bagian kuadrat pertama) y = px² + qx + r …… (bagian kuadrat kedua) Keterangan: a, b, c, p, q, dan r = Bilangan real Menentukan Penyelesaian Sistem Persamaan Kuadrat-Kuadrat Bagaimana cara menyelesaikan sistem persamaan kuadrat-kuadrat itu? Contoh sistem persamaan kuadrat-kuadrat pada umumnya dapat diselesaikan dengan cara tertentu. Berikut langkah-langkah dalam cara menyelesaikan SPKK tersebut yaitu: Melakukan substitusi pada persamaan kuadrat pertama menu
Read more

SAYA SENANG SEKOLAH DI SMAN 63 JAKARTA

Image
Nama : Meidianti Sherli Rahmi           Kelas : X-MIPA 3            No. Absen : 18   “Cerita Tentang Bahagianya Saya Sekolah  Di SMAN 63 Jakarta''   Assalamu'alaikum Warahmatullahi Wabarakatuh. Yang terhormat Ibu Lizza Novrida sebagai guru mata pelajaran Matematika, serta teman-teman dan semua pembaca yang berbahagia. Alhamdulillah, segala puji dan syukur ke hadirat Allah SWT atas limpahan rahmat dan karunia-Nya sehingga kita masih diberi kesehatan dan dapat melaksanakan pembelajaran walaupun dengan daring. Shalawat serta salam semoga tercurahkan bagi Rasulullah SAW bersama keluarga dan para sahabatnya. Hanya dengan karunia Allah SWT saya dapat menyelesaikan tugas yang diberikan Bu Lizza dan dapat bercerita kepada semua pembaca tentang bahagianya Saya Diterima di SMAN 63 Jakarta. Alhamdulillah, saya sangat bersyukur sekaligus bahagia dapat diterima dan menjadi keluarga dari SMA Negeri 63 Jakarta, SMAN 63 Jakarta ini merupakan pilihan terbaik saya dan orang tua s
Read more