SOAL PERSAMAAN DAN PERTIDAKSAMAAN RASIONAL DAN IRASIONAL
Nama : Meidianti Sherli Rahmi
Kelas : X-MIPA 3
Absen :17
Matematika Wajib, SMAN 63 Jakarta
RASIONAL
Soal Persamaan Rasional
1. Tentukan himpunan penyelesaian dari 1/x-3 = 1/4
Penyelesaian : maka x = 7
2. Tentukan himpunan penyelesaian dari persamaa rasional 3x / x + 1 = 2/5
Penyelesaian : maka x = 2/13
3. persamaan rasional x / x + 3 = x + 1 / x - 2 tentukan nilai x yang memenuhi
Penyelesaian :
4. Tentukan himpunan penyelesaian dari persamaan
Penyelesaian :
5. Nilai x yang memenuhi persamaan dibawah ini adalah
Penyelesain :
Soal Pertidaksamaan Rasional
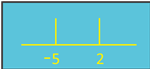
1. Tentukan himpunan penyelesaian dari pertidaksamaan rasional x + 5 / x - 2 < 0
Penyelesaian :
2. tidak terlihat tidak samaan rasional 4/x - 3 3/2x - 1 tentukanlah himpunan penyelesaiannya
Penyelesaia :
3. Tentukanlah penyelesaian dari pertidaksamaan rasional x + 3 / x² - 4 > 0
Penyelesaian :
4. Tentukan himpunan penyelesaian dari 2 - x / x + 1 < 0
Penyelesaian :
5. Tentukan himpunan penyelesaia dari x - 3 / x + 7 1
Penyelesaian :
IRASIONAL
Soal Persamaan Irasional
1. Tentukanlah nilai x
Penyelesaian :
2. Tentukanlah nilai x dari
Penyelesaian :
3. Tentukanlah nilai x dari
Penyelesaian :
4. Tentukanlah nilai x di bawah ini
Penyelesaian :
5. Hasil dari penjumlahan di bawah ini adalah
Penyelesaian :
Soal Pertidaksamaan Irasional
1. Tentukanlah nilai x dari
Penyelesaian :
2. Tentukanlah nilai x yang memenuhi
Penyelesaian :
3. Tentukanlah nilai x yang memenuhi
Penyelesaian :
4. Tentukan nilai x yan memenuhi
Penyelesaian :
5. Tentukan nilai x yang memenuhi
Penyelesaian :
6. Nilai x yang memenuhi adalah
Penyelesaian :
7. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ 16 – x2 ≤ x + 4.
Penyelesaian soal
Syarat pertidaksamaan irasional:
- 16 – x2 ≥ 0.
- x2 – 16 ≤ 0.
- (x – 4)(x + 4) ≤ 0.
- x = 4 dan x = -4
- -4 ≤ x ≤ 4
Kemudian kita kuadratkan pertidaksamaan seperti dibawah ini:
- ( √ 16 – x2 )2 ≤ (x + 4)2
- 16 – x2 ≤ x2 + 8x + 16
- 16 – x2 – x2 – 8x – 16 ≤ 0
- -2x2 – 8x ≤ 0
- 2x2 + 8x > 0
- 2x (x + 4) > 0
- x ≤ – 4 dan x ≥ 0
Lalu kita buat garis bilangan antara syarat dengan hasil diatas sebagai berikut:
8. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ x – 5 < 2.
Penyelesaian soal
Untuk menjawab soal ini kita tentukan terlebih dahulu syarat agar pertidaksamaan irasional berlaku yaitu:
- x – 5 ≥ 0
- x ≥ 5
Selanjutnya kita kuadratkan kedua ruas pertidaksamaan irasional sehingga didapat:
- (√ x – 5 )2 < 22.
- x – 5 < 4
- x < 4 + 5 atau x < 9
Lalu kita buat garis bilangan untuk menentukan irisan antara syarat x ≥ 5 dan x < 9.
9. Tentukan himpunan penyelesaian dari pertidaksamaan irasional √ x – 1 > 2
Penyelesaian :
Syarat yang berlaku pada pertidaksamaan irasional diatas sebagai berikut:
- x – 1 ≥ 0.
- x ≥ 1.
Kemudian kita kuadratkan pertidaksamaan diatas sehingga didapat:
- ( √ x – 1 )2 > 22
- x – 1 > 4
- x > 4 + 1
- x > 5
Jadi himpunan penyelesaian pertidaksamaan ini adalah x > 5.
10. Tentukan himpunan penyelesaian pertidaksamaan irasional dari √ x + 5 < 4
Penyelesaian :
* Pertama, kedua ruas dikuadratkan, sehingga diperoleh pertidaksamaan sebagai berikut:
DAFTAR PUSTAKA
https://edumatik.net/persamaan-dan-pertidaksamaan-rasional/
https://www.catatanmatematika.com/2021/08/materi-persamaan-dan-pertidaksamaan-irasional.html
https://mathcyber1997.com/soal-dan-pembahasan-pertidaksamaan-irasional-bentuk-akar/
https://www.catatanmatematika.com/2021/08/materi-persamaan-dan-pertidaksamaan-rasional.html
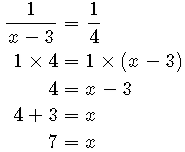




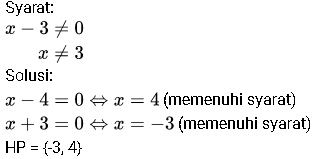
















Comments
Post a Comment