SUDUT-SUDUT BERELASI PADA KUADRAN I, II, III, IV

January 10, 2022

Nama : Meidianti Sherli Rahmi

Kelas : X-MIPA 3

Absen :17

Matematika Wajib, SMAN 63 Jakarta

Definisi Dan Rumus Sudut-Sudut Berelasi Pada Kuadran I, II, III, IV

Sudut Berelasi – Adalah perluasan definisi dasar ilmu trigonometri tentang kesebangunan pada segitiga siku-siku yang memenuhi untuk sudut kuadran I atau sudut lancip (0 − 90°). Sudut berelasi adalah sudut yang memiliki hubungan antara satu dengan yang lain seperti jumlah atau selisihnya. Misal sudut a° dapat dikatakan berelasi dengan sudut – sudut yang besarnya (90°+ a°), (180° + a°), (270°+a°), (360°+a°), atau sudut (-a °).

Dengan memanfaatkan hubungan sudut-sudut, kita dapat menghitung nilai perbandingan pada trigonometri untuk sudut kuadran lainnya, termasuk sudut yang lebih dari 360° dan sudut negatif. Sudut berelasi mencakup 4 kuadran yaitu kuadran I, II, III, dan IV.

Hubungan Sudut Berelasi Di Kuadran I. II. III.IV

Sudut Berelasi Pada Kuadran I

Oleh karena pada gambar di atas, titik M ( x 1 , y 1 ) adalah bayangan dari titik K ( x , y ) oleh pencerminkan terhadap garis y = x , maka:

Untuk α = sudut lancip, maka (90° − α) merupakan sudut-sudut kuadran I. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :

sin (90° − α) = cos α
cos (90° − α) = sin α
tan (90° − α) = cot α

Sudut Berelasi Pada Kuadran II

A. Sudut berelasi dengan sudut (180° - ) atau (π - ).

B. Sudut berelasi dengan (90° + ) atau (π.2 + )

Misalkan A( x , y ) , OA = r , dan AOC = .

Jika diputar dengan pusat perputaran adalah O(0,0) sejauh 90° dengan arah berlawanan dengan arah putar jarum jam, maka bayangan titik A oleh perputaran tersebut adalah A'(- y , x ). Dengan demikian, 'AOA' = (90° + ) dan OA = OA' = r .

Untuk α = sudut lancip, maka (90° + α) dan (180° − α) merupakan sudut-sudut kuadran II. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :

sin (90° + α) = cos α
cos (90° + α) = -sin α
tan (90° + α) = -cot α
sin (180° − α) = sin α
cos (180° − α) = -cos α
tan (180° − α) = -tan α

Sudut Berelasi Pada Kuadran III

A. Sudut berelasi dengan (180° + ) atau (π + )

Mari kita perhatikan gambar berikut.

B. Sudut berelasi dengan sudut (270° - ) atau (32π. - )

Misalkan A( x , y ) , OA = r , dan AOC = .

Jika A dicerminkan terhadap garis y = x , kemudian diputar dengan pusat perputaran adalah O sejauh 180° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A"(-y, -x) , dimana AOA' = ( 270° - ) dan OA = OA" = r .

Untuk α = sudut lancip, maka (180° + α) dan (270° − α) merupakan sudut kuadran III. Dalam trigonometri, relasi sudut dinyatakan sebagai berikut :

sin (180° + α) = -sin α
cos (180° + α) = -cos α
tan (180° + α) = tan α
sin (270° − α) = -cos α
cos (270° − α) = -sin α
tan (270° − α) = cot α

Sudut Berelasi Pada Kuadran IV

A. Sudut berelasi dengan (360° - ) atau (2π - )

B. Sudut berelasi dengan sudut (270° + ) atau (32π. + )

Jika A( x , y ) dengan OA = r dan AOB = titik α diputar dengan pusat O(0,0) sejauh 270° dengan arah berlawanan arah putar jarum jam, maka bayangan dari titik A adalah A'( y , x ) , dimana AOA' = (270° + ) dan OA = OA' = r .

Untuk α = sudut lancip, maka (270° + α) dan (360° − α) merupakan sudut kuadran IV. Dalam trigonometri, relasi sudut-sudut dinyatakan sebagai berikut :

sin (270° + α) = -cos α
cos (270° + α) = sin α
tan (270° + α) = -cot α
sin (360° − α) = -sin α
cos (360° − α) = cos α
tan (360° − α) = -tan α

Ada 2 hal yang harus diperhatikan, yaitu sudut relasi yang dipakai dan tanda untuk tiap kuadran.

1. Untuk relasi (90° ± α) atau (270° ± α), maka :

sin → cos
cos → sin
tan → cot

2. Sedangkan untuk relasi (180° ± α) atau (360° ± α), maka :

sin = sin
cos = cos
tan = tan

Berikut adalah table sudut berelasi sin, cos, tan, cosec, sec, dan cotan di kuadran I, II, III, dan IV.

Tanda masing-masing kuadran:

Kuadran I (0 − 90°) = semua positif
Kuadran II (90° − 180°) = sinus positif, lainnya negatif
Kuadran III (180° − 270°) = tangen positif, lainnya negatif
Kuadran IV (270° − 360°) = cosinus positif, lainnya negatif

Berdasarkan rumus diatas dapat disimpulkan bahwa:

Jika menggunakan komplemen 90° dan 270° maka sin menjadi cos dan sebaliknya, tan menjadi cot dan sebaliknya.
Jika menggunakan komplemen 180° dan °maka sin tetap sin, cos tetap cos dan tan tetap tan.

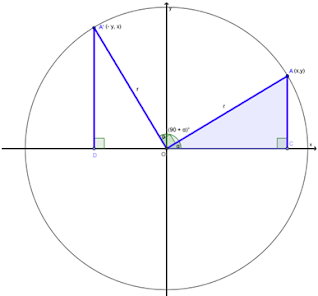
Sudut Berelasi Dengan Sudut (-α)

Pada gambar di atas,

QOP = → berlawanan arah dengan arah putar jarum jam.
QOP' = -α → searah dengan arah putar jarum jam..

Bagaimana dengan nilai perbandingan trigonometri pada batas kuadran? Nilai perbandingan trigonometri pada batas kuadran dapat kita tentukan dengan menggunakan lingkaran satuan.

Bagaimana dengan sudut A yang lebih besar dari 360°?

Jika sudut A lebih besar dari 360°, maka sudut A harus diubah terlebih dahulu sehingga berbentuk (θ + k .360°) dengan k = 1, 2, 3, 4. Dengan demikian: