SPLTV (SISTEM PERSAMAAN LINEAR TIGA VARIABEL)
Nama : Meidianti Sherli Rahmi
Kelas : X-MIPA 3
Absen : 17
Matematika Wajib, SMAN 63 Jakarta
Definisi dan Bentuk Umum Sistem Persamaan Linear Tiga Variabel (SPLTV)
Sistem Persamaan Linear Tiga Variabel (SPLTV) adalah suatu persamaan persamaan yang terdiri dari tiga persamaan linier yang masing-masing persamaannya juga bervariabel tiga. Sistem Persamaan Linear Tiga Variabel (SPLTV) merupakan bentuk perluasan dari Sistem Persamaan Linear Dua Variabel (SPLDV).
Bentuk umum dari Sistem Persamaan Linear Tiga Variabel (SPLTV) yaitu :
Dengan adalah bilangan real.
Ciri – Ciri Sistem Persamaan Linear Tiga Variabel (SPLTV)
Berikut ini merupakan ciri – ciri dari Sistem Persamaan Linear Tiga Variabel (SPLTV) :
- Menggunakan relai tanda sama dengan (=)
- Memiliki tiga variabel
- Variabel ketiga memiliki derajat satu (berpangkat satu)
Hal Hal yang Berhubungan dengan SPLTV
Memuat tiga komponen atau unsur yang selalu berhubungan dengan sistem persamaan linear tiga variabel. Ketiga komponen tersebut yaitu: suku, variabel, koefisien dan konstanta. Berikut ini merupakan penjelasan dari masing-masing komponen SPLTV tersebut.
1. Suku
Suku merupakan suatu bagian dari suatu bentuk aljabar yang terdiri atas variabel, koefisien dan konstanta. Setiap suku yang dipisahkan dengan menggunakan tanda baca maupun pengurangan.
Contoh:
6x – y + 4z + 7 = 0, maka suku–suku dari persamaan tersebut yaitu 6x , -y, 4z dan 7.
2. Variabel
Variabel merupakan peubah atau penggantian dari suatu bilangan yang pada umumnya dilambangkan dengan penggunaan huruf seperti x, y dan z.
Contoh:
Yulisa memiliki 2 buah apel, 5 buah mangga dan 6 buah jeruk. Jika kita menulis dalam bentuk persamaan maka:
Contoh: apel = x , mangga = y dan jeruk = z, sehingga persamannya yaitu 2x + 5y + 6z.
3. Koefisien
Koefisien merupakan suatu bilangan yang menyatakan banyaknya suatu jumlah variabel yang sejenis. Koefisien disebut juga sebagai bilangan yang terdapat di depan variabel, sebab penulisan suatu persamaan koefisien berada di depan variabel.
Contoh:
Gilang memiliki 2 buah apel, 5 buah mangga dan 6 buah jeruk. Jika kita tuliskan ke dalam bentuk persamaan maka:
Contoh: apel = x , mangga = y dan jeruk = z, sehingga persamannya yaitu 2x + 5y + 6z.
Dari persamaan tersebut, maka dapat diketahui bahwa 2, 5 dan 6 merupakan koefisien di mana 2 merupakan koefisien x , 5 merupakan koefisien y serta 6 merupakan koefisien z.
4. Konstanta
Konstanta merupakan sebuah bilangan yang tidak diikuti dengan variabel, sehingga akan memiliki nilai yang tetap atau konstan untuk berapa pun nilai variabel atau peubahnya.
Contoh:
2x + 5y + 6z + 7 = 0, dari persamaan tersebut konstantanya yaitu 7. Sebab, 7 nilai tetap dan tidak terpengaruh dengan berapa pun variabelnya.
Contoh Latihan Soal :
A. Metode Eliminasi.
Soal
Himpunan penyelesaian dari SPLTV di bawah adalah....
2x – y + z = 6
x – 3y + z = –2
x + 2y – z = 3
Langkah 1.
Tentukan variabel apa yang akan kita eliminasi terlebih dahulu. Pada tiga persamaan di atas, peubah yang paling sederhana adalah peubah z sehingga mengeliminasi terlebih dahulu.
Langkah 2.
Dari persamaan 1 dan persamaan 2, diperoleh :
2x – y + 2 = 6
x – 3y + z = –2 –
x + 2y = 8
Dari persamaan 2 dan persamaan 3 diperoleh :
x – 3y + z = –2
x + 2y – z = 3 –
2x – y = 1
Dengan demikian, kita memperoleh SPLDV sebagai berikut.
x + 2y = 8
2x – y = 1
Langkah 3.
Kemudian tentukan nilai x dengan mengeliminasi y. Untuk dapat mengeliminasi variabel y, maka harus menyamakan y dari persamaan kedua.
⇒
x + 2y = 8 → koefisien y = 2
⇒
2x - y = 1 → koefisien y = -1
x + 2y = 8 |× 1| → x + 2y = 8
2x – y = 1 |× 2| → 4x – 2y = 2 +
5x = 10
x = 10/2
x = 2
Kemudian tentukan nilai y dengan mengeliminasi x. Untuk dapat mengeliminasi peubah x, maka harus menyamakan x dari persamaan kedua.
⇒ x + 2y = 8 → koefisien x = 1
⇒ 2x - y = 1 → koefisien x = 2
x + 2y = 8 |× 2| → 2x + 4y = 16
2x – y = 1 |× 1| → 2x – y = 1 –
5 tahun = 15
y = 15/5
y = 3
Untuk mendapatkan nilai z, kita subtitusikan nilai x dan y tersebut ke dalam salah satu SPLTV, misalnya persamaan 2x – y + z = 6 sehingga kita memperoleh:
⇒ 2x - y + z = 6
⇒
2 (2) - 3 + z = 6
⇒ 4-3 + z = 6
⇒ 1 + z = 6
⇒ z = 6-1
⇒ z = 5
Dengan demikian diperoleh nilai x = 2, y = 3 dan z = 5 sehingga himpunan penyelesaian SPLTV di atas adalah {(2, 3, 5)}.
B. Metode Campuran.
Soal
Tentukan himpunan penyelesaian dari
adalah....
Pembahasan :
Misalkan :
Ditanya :
Himpunan penyelesaian dari :
Jawab :
misal :
Metode Campuran (Eliminasi dan subsitusi).
Langkah 1.
Metode Eliminasi :
Eliminasi persamaan 1 dan 2
2p + 2q – 4r = 2
3p – 2q + 5r = 10 +
5p + r = 12 ⇒ Persamaan 4
⇒
Eliminasi Persamaan 1 dan 3
2p + 2q – 4r = 2 | x5 | 10p + 10q – 20r = 10
4p + 5q – 3r =17| x2 | 8p + 10q – 6r = 34 –
2p - 14R = -24 ⇒
Persamaan 5
Kemudian eliminasi kedua persamaan baru yang bervariabel dua tersebut.
⇒
Eliminasi Persamaan 1 dan 3
5p + r = 12 | x2 | 10p + 2r = 24
2p – 14r = –24 | x5 | 10p – 70r = –120 –
72r = 144
r = 144/72
r = 2
Metode Subsitusi :
⇒
Subsitusi Nilai r = 2 Ke Persamaan 4
5p + r = 12
5p + 2 = 12
5p = 12 – 2
5p = 10
p = 10/5
p = 2
⇒
Subsitusi Nilai p = 2 dan r = 2 Ke Persamaan 1
2p + 2q – 4r = 2
2(2) + 2q – 4(2) = 2
4 + 2q – 8 = 2
2q = 2 + 8 – 4
2q = 6
q = 6/2
q = 3
Nilai x, y dan z :
Kesimpulan :
Jadi, himpunan penyelesaian dari
C. Metode Determinan.
Metode determinan sering juga disebut dengan metode cramer. Determinan adalah suatu bilangan yang berkaitan dengan matriks bujur sangkar (persegi). Determinan dapat pula digunakan untuk menemukan sistem persamaan linear baik dua variabel (SPLDV) maupun tiga variabel (SPLTV).
Soal
Tentukan nilai x, y dan z dan himpunan penyelesaian dari SPLTV di bawah ini.
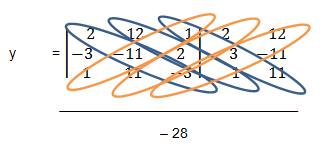
2x + 3y + z = 12
–3x – y +2z = –11
X + 2y – 3z = 11
Pembahasan :
X = (12 x –1 x –3) + (3 x 2 x 11) + (1 x (-11) x 2) + (1 x (-11) x 2) – (11 x (-1) x 1) +
(2 x 2 x 12) + (-3 x -11 x 3)
= (36 + 66 + (-22)) – (-11 + 48 + 99)
= (2 x (-1) x (-3) ) + (3 x 2 x 1) + (1 x (-3) x 2) – (1 x (-1) x 1) + (2 x 2 x 2) +
(3 x (-3) x (-3))
= (6 + 6 + (-6)) – (-1 + 8 + 27)
= (36 + 66 + (-22)) – (-11 + 48 + 99)
/ (6 + 6 + (-6)) – (-1 + 8 + 27)
= (80) – (136) / (6) – (34)
= –52 / –28
X = 2
y = (66 + 24 + 33) – (-11 + 44 + (-108)) / (–28)
= (57) – (141) / –28
= –84 / –28
y = 3
z = (- 22 + (- 33) + (-72)) – (- 12 + (-44) + (-99)) / – 28
= (-127) – (-155) / – 28
= 28 / – 28
z = – 1
DAFTAR PUSTAKA :
1. https://edura.id/blog/matematika/sistem-persamaan-linear-tiga-variabel/
2. https://www.kelaspintar.id/blog/edutech/sistem-persamaan-linear-tiga-variabel-dan-metode-penyelesaiannya-3129/
3. https://www.yurmawita.com/2020/08/persamaan-linear-tiga-variabel-metode.html
4. https://www.madematika.net/2014/09/menyelesaikan-persamaan-linier-tiga.html


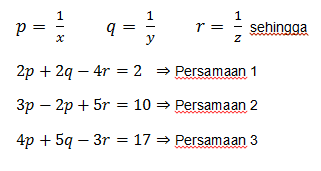










Comments
Post a Comment